USING ENGLISH TO CALCULATE

Stoichiometry

What is a Chemical Equation?

In chemistry, we use symbols to represent the various chemicals. Success in chemistry depends upon developing a strong familiarity with these basic symbols. For example, the symbol "C"represents an atom of carbon, and "H" represents an atom of hydrogen. To represent a molecule of table salt, sodium chloride, we would use the notation "NaCl", where "Na" represents sodium and "Cl" represents chlorine. We call chlorine "chloride" in this case because of its connection to sodium. You should have reviewed naming schemes, or nomenclature, in earlier readings.

A chemical equation is an expression of a chemical process. For example:

AgNO₃(aq) + NaCl(aq) ---> AgCl(s) + NaNO₃(aq)

In this equation, AgNO₃ is mixed with NaCl. The equation shows that the reactants (AgNO₃ and NaCl) react through some process (--->) to form the products (AgCl and NaNO₃). Since they undergo a chemical process, they are changed fundamentally.

Often chemical equations are written showing the state that each substance is in. The (s) sign means that the compound is a solid. The (l) sign means the substance is a liquid. The (aq) sign stands for aqueous in water and means the compound is dissolved in water. Finally, the (g) sign means that the compound is a gas.

Coefficients are used in all chemical equations to show the relative amounts of each substance present. This amount can represent either the relative number of molecules, or the relative number of moles (described below). If no coefficient is shown, a one (1) is assumed.

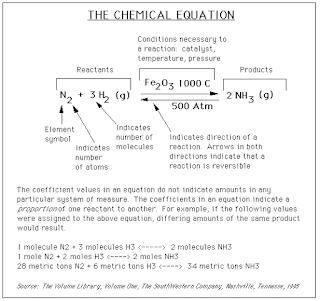
On some occasions, a variety of information will be written above or below the arrows. This information, such as a value for temperature, shows what conditions need to be present for a reaction to occur. For example, in the graphic below, the notation above and below the arrows shows that we need a chemical Fe₂O₃, a temperature of 1000° C, and a pressure of 500 atmospheres for this reaction to occur. The graphic below works to capture most of the concepts described above:

Balancing Chemical Equations

Sometimes, however, we have to do some work before using the coefficients of the terms to represent the relative number of molecules of each compound. This is the case when the equations are not properly balanced. We will consider the following equation:

Al + Fe₃O₄  ---> Al₂O₃ + Fe

Since no coefficients are in front of any of the terms, it is easy to assume that one (1) mole of Al and one (1) mole of Fe₃O₄ react to form one (1) mole of Al₂O₃. If this were the case, the reaction would be quite spectacular: an aluminum atom would appear out of nowhere, and two (2) iron atoms and one (1) oxygen atom would magically disappear. We know from the Law of Conservation of Mass (which states that matter can neither be created nor destroyed) that this simply cannot occur. We have to make sure that the number of atoms of each particular element in the reactants equals the number of atoms of that same element in the products. To do this we have to figure out the relative number of molecules of each term expressed by the term's coefficient.

Balancing a simple chemical equation is essentially done by trial and error. There are many different ways and systems of doing this, but for all methods, it is important to know how to count the number of atoms in an equation. For example we will look at the following term.

2Fe₃O₄

This term expresses two (2) molecules of Fe₃O₄. In each molecule of this substance there are three (3) Fe atoms. Therefore in two (2) molecules of the substance there must be six (6) Fe atoms. Similarly there are four (4) oxygen atoms in one (1) molecule of the substance so there must be eight (8) oxygen atoms in two (2) molecules.

Now let's try balancing the equation mentioned earlier:

Al + Fe₃O₄---> Al₂O₃+ Fe 

Developing a strategy can be difficult, but here is one way of approaching a problem like this. 

1.    Count the number of each atom on the reactant and on the product side. 

2.    Determine a term to balance first. When looking at this problem, it appears that the oxygen will be the most difficult to balance so we'll try to balance the oxygen first. The simplest way to balance the oxygen terms is:

Al + 3 Fe₃O₄ ---> 4 Al₂O₃+ Fe

Be sure to notice that the subscript times the coefficient will give the number of atoms of that element. On the reactant side, we have a coefficient of three (3) multiplied by a subscript of four (4), giving 12 oxygen atoms. On the product side, we have a coefficient of four (4) multiplied by a subscript of three (3), giving 12 oxygen atoms. Now, the oxygens are balanced.

3.    Choose another term to balance. We'll choose iron, Fe. Since there are nine (9) iron atoms in the term in which the oxygen is balanced we add a nine (9) coefficient in front of the Fe. We now have:

Al +3 Fe₃O₄ ---> 4Al₂O₃+ 9Fe

4.    Balance the last term. In this case, since we had eight (8) aluminum atoms on the product side we need to have eight (8) on the reactant side so we add an eight (8) in front of the Al term on the reactant side. 

Now, we're done, and the balanced equation is:

8Al + 3Fe₃O₄ ---> 4Al₂O₃ + 9 Fe

Limiting Reagents

Sometimes when reactions occur between two or more substances, one reactant runs out before the other. That is called the "limiting reagent". Often, it is necessary to identify the limiting reagent in a problem. 

Example: A chemist only has 6.0 grams of C₂H₂ and an unlimited supply of oxygen and he desires to produce as much CO₂ as possible. If she uses the equation below, how much oxygen should she add to the reaction?

2C₂H₂(g) + 5O₂(g) ---> 4CO₂(g) + 2 H₂O(l)

To solve this problem, it is necessary to determine how much oxygen should be added if all of the reactants were used up (this is the way to produce the maximum amount of CO₂). 

First, we calculate the number of moles of C₂H₂ in 6.0 g of C₂H₂. To be able to calculate the moles we need to look at a periodic table and see that 1 mole of C weighs 12.0 g and H weighs 1.0 g. Therefore we know that 1 mole of C₂H₂ weighs 26 g (2 × 12 grams + 2 × 1 gram).

6.0 g C2H2 x

1 mol C2H2 --------------------- (24.0 + 2.0)g C2H2

= 0.25 mol C2H2

Then, because there are five (5) molecules of oxygen to every two (2) molecules of C₂H₂, we need to multiply the result by 5/2 to get the total molecules of oxygen. Then we convert to grams to find the amount of oxygen that needs to be added:

0.25 mol C2H2 x

5 mol O2 -------------- 2 mol C2H2

x

32.0 g O2 --------------- 1 mol O2

= 20 g O2

Percent Composition

It is possible to calculate the mole ratios (also called mole fractions) between terms in a chemical equation when given the percent by mass of products or reactants.

percentage by mass = mass of part/ mass of whole

There are two types of percent composition problems-- problems in which you are given the formula (or the weight of each part) and asked to calculate the percentage of each element and problems in which you are given the percentages and asked to calculate the formula.

In percent composition problems, there are many possible solutions. It is always possible to double the answer. For example, CH and C₂H₂ have the same proportions, but they are different compounds. It is standard to give compounds in their simplest form, where the ratio between the elements is as reduced as it can be-- called the empirical formula. When calculating the empirical formula from percent composition, one can convert the percentages to grams. For example, it is usually the easiest to assume you have 100 g so 54.3% would become 54.3 g. Then we can convert the masses to moles; this gives us mole ratios. It is necessary to reduce to whole numbers. A good technique is to divide all the terms by the smallest number of moles. Then the ratio of the moles can be transferred to write the empirical formula.

Example: If a compound is 47.3% C (carbon), 10.6% H (hydrogen) and 42.0% S (sulfur), what is its empirical formula?

To do this problem we need to transfer all of our percents to masses. We assume that we have 100 g of this substance. Then we convert to moles:

Carbon:	47.3 grams -------------------- 1	x	1 mole ----------------- 12.01 grams	= 3.94 moles
Hyrdrogen:	10.6 grams --------------- 1	x	1 mole ------------- 1.008 grams	= 10.52 moles
Sulfur:	42.0 grams -------------- 1	x	1 mole ---------------- 32.07 grams	= 1.310 moles

Now we try to get an even ratio between the elements so we divide by the number of moles of sulfur, because it is the smallest number:

Carbon:	3.94 ------ 1.310	= 3
Hydrogen:	10.52 ------ 1.310	= 8
Sulfur:	1.310 ------ 1.310	= 1

So we have: C₃H₈ S

Example: Figure out the percentage by mass of hydrogen sulfate, H₂SO₄.

In this problem we need to first calculate the total mass of the compound by looking at the periodic table. This gives us:

2(1.008) + 32.07 + 4(16.00) g/mol = 98.09 g/mol 

Now, we need to take the weight fraction of each element over the total mass (which we just found) and multiply by 100 to get a percentage.

hydrogen:	2(1.008) --------- 98.09	=	2.016 ------ 98.09	= 0.0206 ∗ 100 = 2.06%
sulfur:	32.07 ---------- 98.09	= 0.327 ∗ 100 = 32.7%
oxygen:	4(16.00) --------- 98.09	=	64.00 ------ 98.09	= 0.652 ∗ 100 = 65.2%

Now, we can check that the percentages add up to 100% 

65.2 + 2.06 + 32.7 = 99.96

This is essentially 100 so we know that everything has worked, and we probably have not made any careless errors. 

So the answer is that H₂SO₄ is made up of 2.06% H, 32.7% S, and 65.2% O by mass.

Empirical Formula and Molecular Formula

While the empirical formula is the simplest form of a compound, the molecular formula is the form of the term as it would appear in a chemical equation. The empirical formula and the molecular formula can be the same, or the molecular formula can be any positive integer multiple of the empirical formula. Examples of empirical formulas: AgBr, Na₂S, C₆H₁₀O₅. Examples of molecular formulas: P₂, C₂O₄, C₆H₁₄S₂, H₂, C₃H₉.

One can calculate the empirical formula from the masses or percentage composition of any compound. We have already discussed percent composition in the section above. If we only have mass, all we are doing is essentially eliminating the step of converting from percentage to mass.

Example: Calculate the empirical formula for a compound that has 43.7 g P (phosphorus) and 56.3 grams of oxygen. First we convert to moles:

43.7 grams P ------------- 1	x	1 mol ----------- 30.97 grams	= 1.41 moles
56.3 grams O ------------- 1	x	1 mol -------------- 16.00 grams	= 3.52 moles

Next we divide the moles to try to get an even ratio.

Phosphorus:	1.41 ----- 1.41	= 1.00
Oxygen:	3.52 ----- 1.41	= 2.50

When we divide, we did not get whole numbers so we must multiply by two (2). The answer = P₂O₅

Calculating the molecular formula once we have the empirical formula is easy. If we know the empirical formula of a compound, all we need to do is divide the molecular mass of the compound by the mass of the empirical formula. It is also possible to do this with one of the elements in the formula; simply divide the mass of that element in one mole of compound by the mass of that element in the empirical formula. The result should always be a natural number.

Example: if we know that the empirical formula of a compound is HCN and we are told that a 2.016 grams of hydrogen are necessary to make the compound, what is the molecular formula? In the empirical formula hydrogen weighs 1.008 grams. Dividing 2.016 by 1.008 we see that the amount of hydrogen needed is twice as much. Therefore the empirical formula needs to be increased by a factor of two (2). The answer is: 

H₂C₂N₂.

Concentrations of Solutions

The concentration of a solution is the "strength" of a solution. A solution typically refers to the dissolving of some solid substance in a liquid, such as dissolving salt in water. It is also often necessary to figure out how much water to add to a solution to change it to a specific concentration.

The concentration of a solution is typically given in molarity. Molarity is defined as the number of moles of solute (what is actually dissolved in the solution) divided by the volume in liters of solution (the total volume of what is dissolved and what it has been dissolved in).

Molarity =

moles of solute ------------------ liters of solution

Molarity is probably the most commonly used term because measuring a volume of liquid is a fairly easy thing to do.

Example: If 5.00 g of NaOH are dissolved in 5000 mL of water, what is the molarity of the solution?

One of our first steps is to convert the amount of NaOH given in grams into moles:

5.00g NaOH -------------- 1

x

1 mole ------------------------- (22.9 + 16.00 + 1.008)g

= 0.125 moles

Now we simply use the definition of molarity: moles/liters to get the answer

Molarity =

0.125 moles --------------- 5.00 L of soln

= 0.025 mol/L

So the molarity (M) of the solution is 0.025 mol/L.

Molality is another common measurement of concentration. Molality is defined as moles of solute divided by kilograms of solvent (the substance in which it is dissolved, like water).

Molality =

moles of solute --------------- kg of solvent

Molality is sometimes used in place of molarity at extreme temperatures because the volume can contract or expand.

Example: If the molality of a solution of C₂H₅OH dissolved in water is 1.5 and the mass of the water is 11.7 kg, figure out how much C₂H₅OH must have been added in grams to the solution.

Our first step is to substitute what we know into the equation. Then we try to solve for what we don't know: moles of solute. Once we know the moles of solute we can look at the periodic table and figure out the conversion from moles to grams.

Molality = moles solute -------------- kg solvent

Now we simply use the definition of molarity: moles/liters to get the answer

Molality = moles solute ------------- kg solvent

1.5 mols ------ kg = moles solute ------------ 11.7 kg

1.5 moles ------ kg x 11.7 kg = 17.55 moles

17.55 moles ------------ 1 x (2 ∗ 12.01) + (6 ∗ 1.008) + 16 ---------------------------------- 1 moles = 808.5 g C2H5OH

It is possible to convert between molarity and molality. The only information needed is density.

Example: If the molarity of a solution is 0.30 M, calculate the molality of the solution knowing that the density is 3.25 g/mL.

To do this problem we can assume one (1) liter of solution to make the numbers easier. We need to get from the molarity units of mol/L to the molality units of mol/kg. We work the problem as follows, remembering that there are 1000 mL in a Liter and 1000 grams in a kg. This conversion will only be accurate at small molarities and molalities.

0.3 mol ---------- 1 L

x

1 mL ------ 3.25 g

x

1 L -------------- 1000 mL

x

1000 g -------- 1 kg

= 0.09 mols / kg

It is also possible to calculate colligative properties, such as boiling point depression, using molality. The equation for temperature depression or expansion is

ΔT= K_f × m

Where:

ΔT is temperature depression (for freezing point) or temperature expansion (for boiling point) (°C)

K_f is the freezing point constant (kg °C/mol)

m is molality in mol/kg

Example: If the freezing point of the salt water put on roads is -5.2° C, what is the molality of the solution? (The K_f for water is 1.86 °C/m.) 

This is a simple problem where we just plug in numbers into the equation. One piece of information we do have to know is that water usually freezes at 0° C.

ΔT = K_f * m
ΔT/K_f = m
m = 5.2/1.86
m = 2.8 mols/kg